Differential

Differential Calculus is used to find the slope of a function at any given point, as an example, let's say we have the following function:
f(x) = 3x + 2
What if we wanted to know the slope at the point x = 4?
This is the type of function differential calculus allows us to solve.
Let's see what the y value is when x = 4, if we substitue x for 4 we can see: 3 * 4 + 2 = 14.
What if we inputted a value just slightly higher? if we input 4.5, we can see: 3 * 4.5 + 2 = 15.5
if we subtract the first from the second we get 15.5 - 14 = 1.5, based on the fact that we inputted 0.5, we can see that y is increasing 3 times as fast as x.
What if we have a more complex example?
As an example, the function e^x, if we input a value as large as 0.5 extra it will cause problems as instead of giving an actual slope, you will get back an average slope between the position x and x + 0.5, what if we input a smaller number such as 0.01?
Let's give it a shot, let's say we want to find the slope at x = 4, we can see based on the function that the value is e⁴ = ~54.6, we can however see that when we input x = 4.01, we get ~55.147

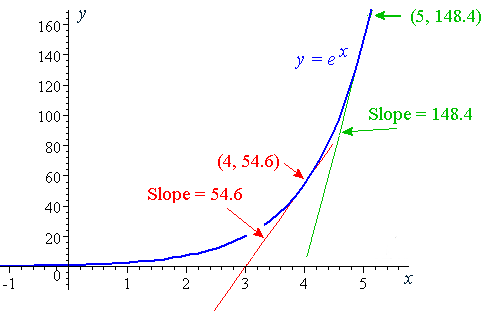
if we subtract 54.6 from 55.147 we get 0.547, so we can see that y gains 0.547 for 0.01 increase in x at x = 4.
There are many different rules that simplify differentiation, a list can be found here.

Integral

Integration can be used to find ares made by functions.
Instead of having to add up hundreds, even thousands of numbers of very small value, we can just consider the fact that integration is the reverse of differentiation. When dealing with slopes, adding constants does nothing for us, we can see in the first differentiation example, we added 2, and it did not affect the slope. However, when calculating areas, adding a constant does matter. therefore when integrating, we must always add C.
Integration, like differentiation, has rules, these can be found here

Vector

Vector calculus is the differentiation, and integration of 3 dimensional functions.
Some of the functions include vector addition, scalar multiplication, the dot production, and the cross product.